MATEMÁTICOS
 | ARQUETIPOS MATEMÁTICOS |
| Nivel | Categoría de Números |
| Consciente (expresable) | Naturales |
| Enteros | |
| Racionales | |
| Consciente-Inconsciente | Irracionales expresables |
| Inconsciente (inexpresable) | Irracionales inexpresables |
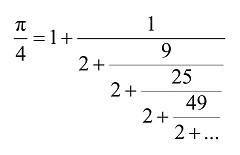
|
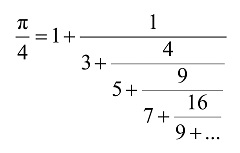
|
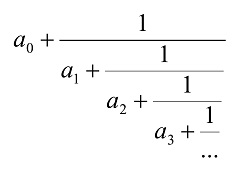
|
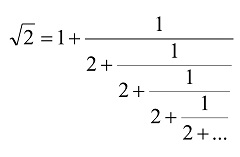
|
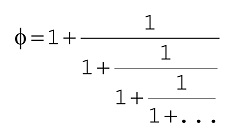
|
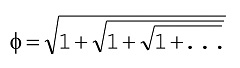
|

|
| Tetraktys pitagórica |